안녕하세요 오늘은 기둥의 하중-모멘트 상관도(P-M곡선)에 대해서 글을 작성해 보겠습니다. 실제 기둥은 축력, 휨모멘트, 전단력을 동시에 받습니다. 여기서 축력과 휨모멘트가 동시에 작용할 때, 기둥이 견딜 수 있는 최대 하중 상태를 나타내는 그래프가 하중-모멘트 상관도입니다.
기둥 단면의 파괴될 때 변형률이 어떻게 분포하는지 확인하고 이것으로부터 축하중과 편심거리에 따른 단면의 축하중 강도 변화를 보여주는 하중-모멘트 상관도를 작도할 수 있습니다.
이러한 상관곡선은 아래와 같은 특징으로 구분할 수 있습니다.
- 순수 압축하중 작용점
- 압축파괴 구간(압축지배)
- 균형파괴점
- 인장파괴 구간(변화구간, 인장지배)
- 순수 휨모멘트 작용점
기둥의 하중-모멘트 상관도 특징을 아래의 그림을 기준으로 설명드리겠습니다.

- A점 : 휨모멘트가 0으로 순수한 압축력만 작용하는 상태입니다.
- B점 : 최외단 인장철근의 변형률이 압축변형률에서 인장변형률로 바뀌는 시점입니다. 즉, 변형률이 0인지점입니다.
- C점 : 최외단 인장철근 변형률이 항복변형률에 도달하는 상태입니다. 이 지점을 균형변형률 상태 혹은 균형파괴상태라고 합니다.(최외단 인장철근이 항복할 때 압축연단 콘크리트가 극한변형률에 도달)
- D점 : 최외단 인장철근 변형률이 항복변형률의 2.5배가 되는 시점으로 인장지배 구간에 기준이 되는 지점입니다.
- E점 : 휨모멘트가 점점 증가하여 축하중은 0이 되는 상태로 휨모멘트만 존재하는 휨 거동을 하는 보가 됩니다.
하지만 이것은 공칭강도에 따른 이론상관도(theoretical interaction or nominal interaction)입니다. 실제 설계에서는 적절한 강도감소계수를 곱하여 설계상관도(design interaction)에 따라 설계강도를 산정해야합니다.
강도감소계수는 다음과 같이 산정할 수 있으며 해당 내용을 반영하여 설계상관도를 작도합니다.
- 압축지배구간

- 변화구간
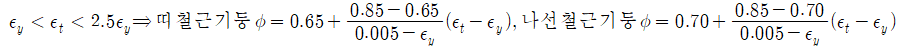
- 인장지배구간
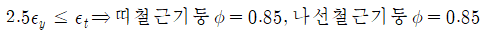
- 이론상관도와 설계상관도

여기서, 설계상관도 윗부분이 축강도가 일정한부분이 존재합니다. 이 이유는 기둥에 순수 축하중만 작용하거나 압축력과 매우 작은 휨모멘트가 작용하는 경우에 기둥의 최대 축강도를 제한하기 위해서입니다. 그이유는 다음과 같습니다.
- 해석에 예측하지 못한 편심이 작용할 수 있으므로 축하중을 제한하여 편심으로 인한 모멘트에 저항하기 위함
- 지속적으로 높은 하중이 작용할 때 콘크리트의 압축강도가 설계압축강도보다 작게 될 가능성을 고려하기 위함
위와 같은 이유로 순수압축상태의 공칭강도를 80%(띠철근기둥), 85%(나선철근기둥)로 직접적으로 제한하고 있습니다.
오늘은 기둥의 하중-모멘트 상관도(P-M곡선)에 대해서 글을 작성해 보았습니다. 해당 내용은 기둥부재를 공부하신다면 필수적으로 이해하고 넘어가야 합니다. 축력과 휨모멘트가 동시에 작용하는 부재는 설계상관도의 허용범위 안에서 작용해야 안전한 설계가 되는 것입니다! 다음에 기회가 된다면 해당내용의 예제를 풀어보겠습니다. 오늘도 글을 읽어주셔서 감사합니다😁
'콘크리트' 카테고리의 다른 글
| 2축 휨을 받는 기둥: 실제 기둥은 대부분 2축 휨을 받는다. (0) | 2024.09.13 |
|---|---|
| P-M 상관곡선 관련 예제 풀이 (0) | 2024.09.10 |
| 철근콘크리트 단면의 소성중심(Plastic Centroid) : 편심거리 및 관련 예제 풀이 (0) | 2024.08.29 |
| 횡방향 철근(후프근)으로 구속된 압축부재의 횡구속 효과(KDS 14 20 20) (0) | 2024.08.13 |
| 모멘트 재분배 : 연속 휨부재는 모멘트가 재분배가 제한적으로 가능하다. (0) | 2024.08.03 |


