안녕하세요 오늘은 건축물에 가장 많이 쓰이는 콘크리트 재료 성질에 대해서 포스팅을 해보도록 하겠습니다. 실제로 콘크리트는 건축을 한다면 제대로 알아야 하는 재료입니다. 하지만 콘크리트는 생각보다 복잡한 성질을 가지고 있는 재료입니다. 콘크리트는 시멘트, 물, 모래, 자갈, 혼화재 등으로 이루어진 비균질 재료(heterogeneous material)이기 때문에 각 구성 요소들은 물리적, 화학적 특성이 서로 다르므로 실험적인 내용으로 정립된 개념들이 상당히 많습니다.
콘크리트의 각 부분에서 시멘트, 모래, 자갈의 분포가 균일하지 않을 수 있습니다. 이는 콘크리트가 완벽하게 균일하게 혼합되기 어렵기 때문입니다. 콘크리트가 경화되면서 수축과 팽창이 일어나는데, 이러한 변화가 일관되게 발생하지 않을 수 있습니다. 특히, 골재와 시멘트 페이스트 사이의 접합 부위에서 차이가 발생할 수 있습니다. 이것 외에도 다양한 요소들로 콘크리트 재료의 복잡성은 큽니다. 하지만 일반적인 구조적 분석과 설계에서는 콘크리트를 균질 재료로 가정합니다. 이는 실질적인 설계와 계산의 편의를 위해서입니다. 이러한 균질 재료로 정의하기 위해서 많은 연구자가 실험을 통해 보수적인 실험식을 제안하고 우리는 그러한 식을 적용된 균질 재료로 가정하여 계산합니다.
시멘트, 골재, 물, 공기, 혼화재료에 대한 내용은 따로 다루지 않고 콘크리트 강도에 관한 이야기를 먼저 작성해 보겠습니다. 오늘 포스팅할 내용은 아래와 같습니다.
-압축강도
-탄성계수
-배합강도
-설계기준강도
-인장강도
-2축 및 3축강도
[압축강도(Compressive Strength)]
압축강도는 콘크리트의 가장 중요한 역학적 성질입니다. 콘크리트의 압축강도는 습윤 양생한 재령 28일 표준공시체를 1축 압축하중을 가하여 파괴될 때의 값으로 결정합니다. 만약 표준공시체가 아닌 ϕ100mm x 200mm 공시체를 사용하면 0.97의 보정계수를 곱하면 됩니다.
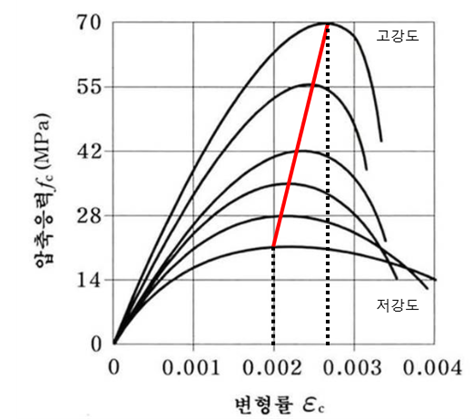
공시체의 1축 응력-변형률 곡선으로 다음과 같은 내용을 알 수 있습니다.
-강도와 파괴변형률의 관계 : 강도가 낮을수록 연성도가 높아짐
-강도와 초기강성의 관계 : 강도가 높을수록 초기강성은 증가하지만, 연성은 감소
-보통강도(40MPa이하) 콘크리트의 변형률 : 최대 응력에서 변형률이 대략 0.002
[탄성계수(Modulus of Elasticity)]
탄성계수는 1축 하중실험에서 콘크리트의 응력-변형률 곡선의 기울기로 결정됩니다. 실제로는 응력-변형률 곡선이 비선형이기 때문에 탄성계수도 일정한 값이 아닌 비선형적인 값을 가지게 됩니다. 하지만 구조해석의 편의성을 위해 탄성계수를 일정한 값으로 설계를 수행합니다.
보통 탄성계수는 다음과 같은 방법으로 결정합니다.
-접선계수(tangent modulus) : 곡선의 어떤 점에서 응력-변형률 곡선의 접선 기울기로 결정
-할선계수(secant modulus) : 원점 혹은 임의 기준점과 기준이 되는 응력의 값을 연결하는 직선의 기울기로 결정
보통 설계에서 사용되는 탄성계수는 할선계수 방식을 이용하여 결정되며 ACI 구조기준에 의하면 0.45fck와 0점을 연결하는 직선의 기울기를 Ec로 사용합니다. 접선계수의 경우에는 초기접선계수를 구할 때 사용되는 방식으로 초기접선계수는 지진이나 충격하중이 작용하는 경우의 구조해석에서 이용되는 것으로 알고 있습니다. 일반적으로 초기접선계수는 정적탄성계수에 비해 20%~40% 정도 높지만, 우리나라 KDS 기준에서는 보수적으로 18% 정도 높게 계산하는 것으로 명시되어 있습니다. 그렇다면 콘크리트의 탄성계수 Ec를 계산하는 식에 대해서 알아보도록 하겠습니다.

위의 식은 콘크리트의 단위 질량 mc 의 값이 1,450~2,500kg/m^3인 콘크리트의 경우에 사용하며 fcm의 값은 재령 28일의 평균 압축강도로 fcm = fck + △f 를 통해 산정할 수 있습니다.
여기서, △f는 fck의 값에 의해 결정되며 아래와 같이 결정할 수 있습니다.

또한, 보통중량골재(mc = 2,300kg/m^3)를 사용한다면 아래의 간략식을 사용할 수 있습니다.
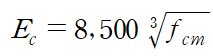
실제로 실무에서는 위의 식을 자주 사용합니다.
콘크리트의 초기접선탄성계수(Eci)는 다음과 같은 식으로 구할 수 있습니다.

[배합강도(Required Average Compressive Strength, fcr]
배합강도는 설계기준강도 fck의 적절한 값을 현장에서 얻기 위해서 생산되는 배합강도를 설계기준강도보다 크게 만들어서 실제로 현장에서 사용되는 콘크리트의 강도가 설계기준강도보다 작아지지 않도록 하기 위한 강도라고 생각하면 될 것 같습니다.
여기서, 배합강도는 30회 이상의 현장강도 시험기록을 근거로 한 표준편차 s를 결정할 수 있다면 아래의 식으로 배합강도를 결정할 수 있습니다.

만약에 15회~29회인 경우 계산된 표준편차에 아래의 보정계수를 곱해야 합니다.
| 시험 횟수 | s 보정계수 |
| 15회 | 1.16 |
| 20회 | 1.08 |
| 25회 | 1.03 |
| 30회 | 1.00 |
| 사이 값은 선형보간 | |
만약 14회 이하인 경우에는 아래의 식을 따라야 합니다.
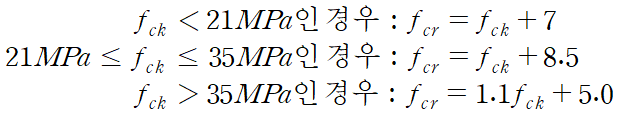
[설계기준강도(Specified Compressive Strength)]
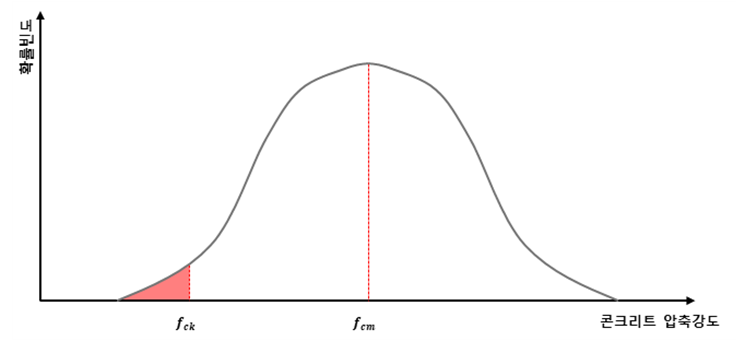
설계기준강도는 말 그대로 구조설계를 수행할 때 사용되는 콘크리트 강도입니다. 실제로 현장에서 타설되는 배합강도는 이 강도보다 커야 합니다. 이러한 이유는 동일한 배합으로 만들어진 콘크리트를 실험해보면 압축강도가 동일하지 않습니다. 이것은 콘크리트가 비균질재료(heterogeneous material)이기 때문입니다. 그러므로 건축구조기준에서는 안전율을 확보하기위해 측정된 콘크리트 압축강도 평균값의 하위 5%를 콘크리트 설계기준강도로 정의하여 구조물을 설계합니다.
[인장강도(Tensile Strength)]
1축 인장하중에서 콘크리트의 응력-변형률 관계는 압축응력에 비해 매우 작은 응력범위를 나타냅니다. 하지만 균열이 일어나기 전까지는 거의 직선에 가까운 응력-변형률 관계를 보여줍니다. 실험에 의하면 콘크리트의 인장강도는 압축강도에 대략적으로 10%입니다. 인장강도가 작은 이유중 가장 큰 이유는 콘크리트에는 아주 미세한 균열단면이 존재하기 때문입니다. 콘크리트에는 미세한 공기층이 분포하고 이러한 공기층이 콘크리트 단면에 공극으로 존재합니다. 압축하중이 작용할 때는 이러한 빈 공간이 닫치게 되어 균열 단면과 비균열단면에서 응력의 전달에 차이가 없습니다. 하지만 인장하중에서는 오직 비균열단면을 통해서만 하중을 전달되어 유효단면적이 줄어듭니다. 그러므로 인장강도가 압축강도에 비해 상당히 작게 측정됩니다.
콘크리트의 인장강도를 측정하는 방법은 할렬실험, 휨실험이 있는데 이러한 실험을 하는 이유는 공시체를 1축 인장실험을 하는 것은 어려우므로 대체적인 방법으로 할렬실험과 휨실험을 수행하여 인장강도를 확인합니다.
-할렬시험
쪼갬인장강도(할렬강도, splitting strength) fsp는 아래와 같이 실험합니다.

쪼갬인장강도는 다음과 같이 구할 수 있습니다.
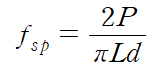
-휨 강도시험
휨강도시험은 150mm X 150mm X 530mm의 장방형 무근콘크리트 보를 3등분점 하중법에 의해서 보가 파괴될 때까지 하중을 작용시켜서 보의 바닥에서의 최대인장응력을 측정하는 시험입니다. 이때의 인장응력을 파괴계수(modulus of rupture) fr로 부릅니다.
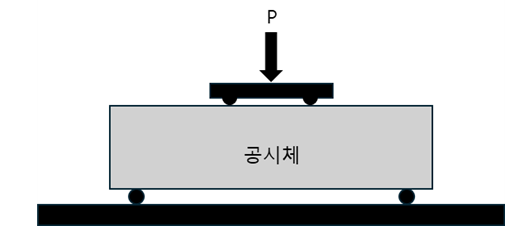
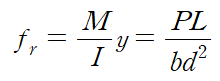
건축구조기준에서는 파괴계수를 실험결과를 토대로 설계기준강도와의 관계로 표현될 수 있도록 정의하였습니다.

여기서 λ는 경량콘크리트계수로 보통콘크리트인 경우 1.0을 사용합니다.
[2축 및 3축 강도]
실제로 설계에서 구조부재들은 2축 및 3축으로 응력이 작용하는 상태로 봐야 합니다. 기둥과 보는 횡구속으로 인해서 횡구속 효과를 고려해야 하고 횡구속이 되어있다는 것은 2축 및 3축 강도를 사용하는 것이 타당하다고 보입니다. 횡방향 철근으로 구속된 부재의 응력-변형률 관계는 KDS 14 20 20을 통해 확인할 수 있습니다. 실험적인 내용을 근거를 들어서 2축 강도가 어떻게 나타나는지 글을 작성해 보도록 하겠습니다.

위의 그래프를 보면 f1과 f2가 동시에 압축이 발생하면 약 20% 정도 강도가 향상됨을 확인할 수 있습니다. 반대로 한쪽 면에는 인장이 작용하고 한쪽 면에는 압축이 작용하면 압축강도가 급격히 줄어드는 것을 확인할 수 있습니다. 상식적으로 생각해보면 당연할 수 있습니다.
3축 응력 하에서의 공시체 응력-변형도를 살펴보면 3축으로 압축이 작용할 때 큰 강도와 연성도가 나타남을 확인할 수 있습니다. 즉, 횡구속 여부에 따라 연성능력을 증가시켜 지진과 같은 횡방향 하중에 대해서 에너지 흡수능력이 대폭 증가함을 알 수 있습니다. 그러므로 지진에 대해서 잘 저항하기에서는 횡구속 철근이 촘촘한 것이 좋을 수 있습니다.
오늘은 건축재료 중에서 가장 보편적으로 사용되는 콘크리트에 대해서 알아보았습니다. 그중에서 강도와 관련된 내용을 중점적으로 다루었는데 이러한 재료의 역학적 성질을 잘 알고 있어야 재료의 물성과 관련된 비선형 특성을 이해하는데에도 도움이 됩니다. 오늘도 글을 읽어주셔서 감사합니다. :)
'콘크리트' 카테고리의 다른 글
| 철근콘크리트 부재의 균열단면2차모멘트 : 균열 전과 후에 따른 단면2차모멘트 다르다 (0) | 2024.06.23 |
|---|---|
| 휨 부재의 강도감소계수 : 부재의 연성능력을 고려한 강도감소계수의 결정 (0) | 2024.06.19 |
| 보 부재의 휨 거동에 대해서 : 인장파괴의 유도가 중요! (0) | 2024.06.17 |
| 철근콘크리트의 내구성(KDS 14 20 40) : 오래가는 구조물을 만들기 위한 설계기준 (0) | 2024.06.14 |
| 콘크리트 재료 성질에 대한 이해 : 콘크리트의 체적변화 편 (0) | 2024.06.13 |



